
9月13日(周二)
阿拉丁第十一期微課和大家分享交流了
光束角相同的燈具光學性能是一樣嗎?
講師:

以下是本次微課PPT全程回顧
提要
·光束角相等情形下多種配光曲線的可能性
·配光曲線的數學表達式
·四種不同配光曲線的燈具產生的光斑對比
·小結

第一部分內容,光束角相同的時候,是不是有多種配光曲線的可能性,大家做設計的時候經常會有這樣的一些討論,用的是多大光束角的?寬光束還是窄光束?還是中光束?討論的時候會有一個疑問,同樣的光束角,比如說15度、30度,是不是它的配光曲線就會有多種形式呢?
這一個圖片內容也是講做這項工作的目的,想讓大家更好地認識光束角這個概念,然后可以在實際的設計中有所幫助,能知其然更知其所以然。

四種典型的配光曲線形狀
為了便于比較,我們這里做的研究是以30度光束角為例的。這里也是為了簡化問題,非對稱的燈具我們這里不討論,只討論軸對稱的配光,所有的條件應該是一樣的,只是配光曲線的形狀不一樣,光束角肯定都是30度。假設的功率每個燈具都是10w,燈具的效率是72%,初始光通量1000的時候,整個流明輸出數是720,這里有些人可能沒有想那么多,但是我這里列了其中的各種可能性,其中的4種配光曲線。當然如果真正理解這篇文章以后,同樣的光束角,比如說30度,你就知道它的可能性可能非常多,甚至是無窮無盡的這種配光曲線的形狀。
“Microsoft Mathematics”軟件界面
為了分析這個問題,我們需要借助一個叫Microsoft Mathematics的一個軟件。為什么要接觸這個軟件呢?因為我們要研究各種配光的形式,然后給它數學化、數字化,用一個代數表達式來表達各種配光。針對我們上一張圖提的這四種配光曲線的形狀,我們列了四種光強的表達式,對每一種光強的表達式都做一個檢驗,看它的光束角是不是真是30度。
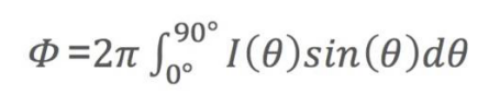
精準計算光通輸出量
可以有這樣的公式,用光強的表達式來計算光通的輸出量,是不是720流明。關于這個流明輸出數的Φ值, I(θ)就是一個光強的數學表達式,這個數學表達式畫成圖形以后就是這個燈具的配光曲線。它需要乘以一個sin(θ)再積分,得出的結果就是流明的輸出數,就是Φ值。
大家理解成,一個配光曲線圍合成一定的面積,光通輸出量就是流明數,它是面積,因為積分的概念就是把這些面積相加,就是整個圍合的面積,但是這里乘以一個sin(θ)角,相當于θ=0的時候,sin(θ)是0;90度時候是1,相當于這個影響因子就是0度的時候小一點,角度越大影響值越大。
關于這個公式的推導過程,很多文獻上有記載,因為是軸對稱,也做了一些簡化,經過若干簡化以后,它是從0度到90度積分,向一個單方向發光,所以說它不積90度以上的角度。這個公式的推導過程以及符號意義,可以參考我在《照明設計》NO.52,2012.7/8上的短文:照明與數學。
這篇文章是2012年完成的,當時比較流行的一個詞就是跨界。我也玩了一把跨界,就是想能不能把數學的一些知識應用到照明里邊來把照明做得更精確化、更數字化。雖然照明是一個感性的東西,但是理性地分析在某些情形下,特別是功能照明也必不可少。
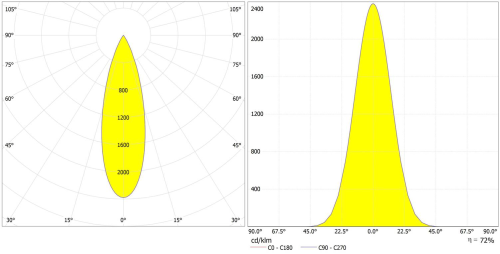
30度光束角的單峰形配光曲線
下面我們就介紹這四種配光曲線。首先第一種叫單峰形配光曲線,說單峰可能后邊還有雙峰或者其它的一些結果。這種配光曲線應該是大家最常見的,也是燈具最多形式的一種配光曲線。這個配光曲線有什么特點?一個是兩種顏色,它是重合的,紅色和藍色,0到180、90、270,說明它是對稱的。再一個它燈具的效率是72%,在右下角是有說明的,這個配光曲線的形狀也是根據后一頁的數學表達式的程序來自動算的。
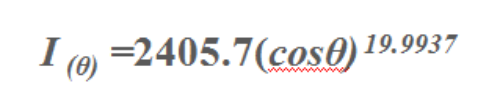
數學表達式
上面這個公式就是配光曲線的一個數學表達式,它應該是cosθ角的一個冪函數。為什么是這樣的一個形狀?也可以翻看一下《照明設計》,就剛才提到的那篇文章。
下面三行算了一下最大光強。就是當θ=0度角度的時候,最大光強的坎德拉值,把15度角代進去算出15度角的時候,它剛剛好等于最大光強的一半值,所以說兩個15度是30度,因此這個配光曲線的光束角就是30度。通過前面的一個積分的公式,也可以算出流明的輸出率,輸出的數值剛好是720流明。后面我會列出其它三種形式的最大光強值,15度角時候的光強還有流明輸出數,都可以一一來驗證整個前面的一些想法。

30度光束角的單峰形配線光曲
這個配光曲線形狀就是我們說的是雙峰形,前面是單峰形,這里是雙峰形,形狀略有一點不一樣,通俗一點講就像我們中國很多地方有筆架山,中間可以放一只筆的這種形狀,兩邊略高一點中間反倒低一點的一個形狀。








